有考生问及这样的问题：《2012考研数学复习大全》理工类350页有关于“向量组的秩和极大无关组的求(证)法”，其中种方法就是“以每个向量为列构成矩阵，然后对矩阵进行行初等变换变成行阶梯形矩阵，设此矩阵的秩为r，则变换后的矩阵中r个线性无关的列向量对应的原向量组即是它的极大无关组，极大无关组含向量的个数即为它的秩”，这种方法用起来简单方便，但是如何来理解它呢?在例11注1中说“A的任意k个列向量与B中对应的k个列向量有相同的线性相关性”(B是由A经过行初等变换而得)，这个结论是怎么来的?

　　事实上，《工程数学线性代数》第三版106页用了一个例子来说明如何利用行初等变换法得到向量组的极大无关组以及如何将其余向量用极大无关组线性表示的，但最后也提出了一个问题：请读者想一想为什么?方法简单实用，但问题是：进行行初等变换后所得行阶梯每一级取一个向量为什么就是原向量组的极大无关组?其他向量线性表示为什么可以根据行最简形矩阵写出?

　　我们将以上问题简化为两个：一是为什么初等行变换不改变列向量的线性相关性?二是列向量进行初等行变换后，为什么可以根据行最简形矩阵写出不属于极大无关组的向量用极大无关组表示的表示式?

　　个问题

　　设α1，α2，…，αn是n个m维列向量，则它们的线性相关性等价于线性方程组AX=0(其中A=(α1，α2，…，αn)，X=(x1，x2，…，xn)T)是否有非零解，即α1，α2，…，αn线性相关等价于AX=0有非零解，α1，α2，…，αn线性无关等价于AX=0只有零解。而对A进行三种行初等变换分别相当于对线性方程组中的方程进行：两个方程交换位置，对一个方程乘一个非零常数，将一个方程的常数倍对应加到另一个方程上。显然进行三种变换后所得方程组与原方程组同解，若设所得方程组为BX=0，则B即为对A进行行初等变换后所得矩阵。B的列向量的线性相关性与BX=0是否有解等价，也就是与AX=0是否有解等价，即与A的列向量的线性相关性等价!

　　第二个问题 以一个具体例子来说明。

　　例(教材上的例题)：设矩阵 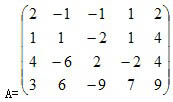，求A的列向量组的一个极大无关组，并把不属于极大无关组的列向量用极大无关组线性表示。

　　解：对A施行初等行变换变为行阶梯最简形矩阵

   

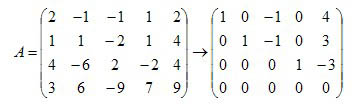
　　显然变换后矩阵的第1、2、4列是3个线性无关向量，而加入第3、5列中任何一列即变为线性相关了，故由行变换不改变列向量的线性相关性可知α1，α2，α4是A的列向量组的极大无关组。

　　那么将α3由α1，α2，α4的线性表示的系数即为非齐次线性方程组

　　(α1，α2，α4)(x1，x2，x3)T=α3的解，故对增广矩阵进行行初等变换即为

   

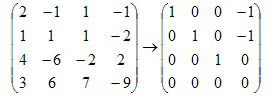
　　所以α3=-α1-α2+0α4，此系数即为对A进行行初等变换后的第3列数字!

　　同理可得α5由α1，α2，α4线性表示的系数即为对A进行初等行变换后所得行最简形矩阵的第5列对应数字。

　　综上所述，对矩阵的行初等变换的理解均可以对应到以此矩阵为系数的线性方程组的同解操作，而讨论线性方程组的解时又可以利用矩阵的相关理论进行简化!