2017考研数学:二元函数极值充分条件的简易证明
文都考研
中
多元函数的极值在实际中有着广泛的应用，在 考研数学中也是一个重要的考点，尤其是二元函数的极值问题。关于二元函数极值的充分条件，在一般高等数学教材和考研复习资料中，要么只是简单介绍一下而不给出证明，要么证明比较繁琐，这使很多同学不能很好地理解充分条件，只能死记硬背，在这里文都蔡老师给大家提供一种简易的证明方法，相信有助于各位2017考研的同学理解和学习。
在证明之前，先回顾一下一元函数的泰勒公式和二元函数的极值定义。
一、一元函数的二阶泰勒公式
在上面的证明过程中，我们主要是利用一元函数的泰勒公式和拉格朗日中值定理，以及关于抛物线的简单性质，没有利用二元函数的泰勒公式，证明方法相对来说比较简捷。最后说明一下，如果判别式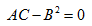
，一般需结合极值的定义来判别是否为极值点。
| *** 热点推荐 *** | |
|
|
| *** 复习必看 *** | |
|
|
2016考研成绩查询与复试分数线专题【版权声明】
本文版权属本网所有，任何媒体、网站或个人未经本网协议不得转载、链接、转贴或以其他方式复制发表。已经本站协议的媒体、网站，在下载使用时必须注明“稿件来源：文都教育”，违者本站将依法追究责任。