2017考研数学:曲线拐点的判别方法分析
函数是高等数学的研究对象,函数的特性包括分析特性和几何特性,分析特性包括函数的、函数的连续与间断、函数的导数、函数的积分等,几何特性包括曲线的图形、曲线的切线和法线、曲线的凹凸性、曲线所围成的面积等,其中曲线的凹凸性是反映曲线的弯曲方向的,如果曲线向下弯曲,则称之为凸,如果曲线向上弯曲,则称之为凹,如果曲线在某点的弯曲方向发生改变,则称该点为拐点,拐点是考研数学的一点考点,如何判别曲线的拐点,下面文都考研数学老师对此做些分析总结,供各位2017考研的考生复习参考。
一、拐点的定义

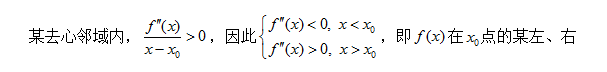




在前面的分析和例题中,我们介绍了曲线拐点的三种判别方法,一种是根据几何图形的弯曲方向是否改变来进行判别,一种是根据函数的二阶导数的符号在某点左右是否改变来判别,第三种方法是根据三阶导数在某点不为零来判别,这三种方法用得较多的是第二种,但在某些情况下用另外两种可能更方便,同学们在实际解题时要灵活运用。
| *** 热点推荐 *** | |
|
|
| *** 复习必看 *** | |
|
|
【版权声明】
本文版权属本网所有,任何媒体、网站或个人未经本网协议不得转载、链接、转贴或以其他方式复制发表。已经本站协议的媒体、网站,在下载使用时必须注明“稿件来源:文都教育”,违者本站将依法追究责任。


