考研数学必考知识点拉格朗日中值定理:有限增量形式
文都考研网整理
中
同学们，使用中值定理解题是考研数学考试常考的一种题型，所以考研数学的几大中值定理是需要我们重点掌握的知识点。本篇文章，文都考研将为同学们整理了考研数学使用拉格朗日中值定理的有限增量形式，希望可以为同学们提供帮助。
考研数学拉格朗日中值定理-有限增量形式：
如果y=f(x)在x的邻域内可导，x+△x也属于该邻域，则存在θ∈(0,1)，使得
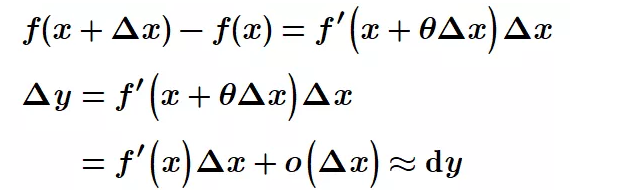
如果f(x)在(a,b)内可导，x，x0∈(a,b)，则在x和x0之间至少存在一点ξ，或存在θ∈(0,1)，使得
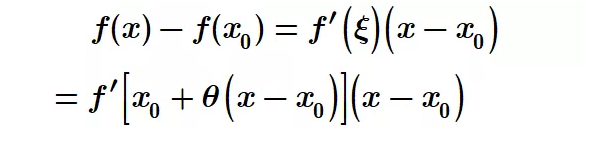
【注】：拉格朗日中值定理架起了函数值、导数值和自变量的取值之间的桥梁.
推论：如果f(x)在(a,b)内恒有f’(x)=0，则在(a,b)内f(x)恒为常数.
以上是关于考研数学拉格朗日中值定理的有限增量形式的具体内容，拉格朗日中值定理是考研数学的重点知识，同学们一定要掌握。文都考研会继续更新2020考研数学备考知识，欢迎广大考生持续关注！